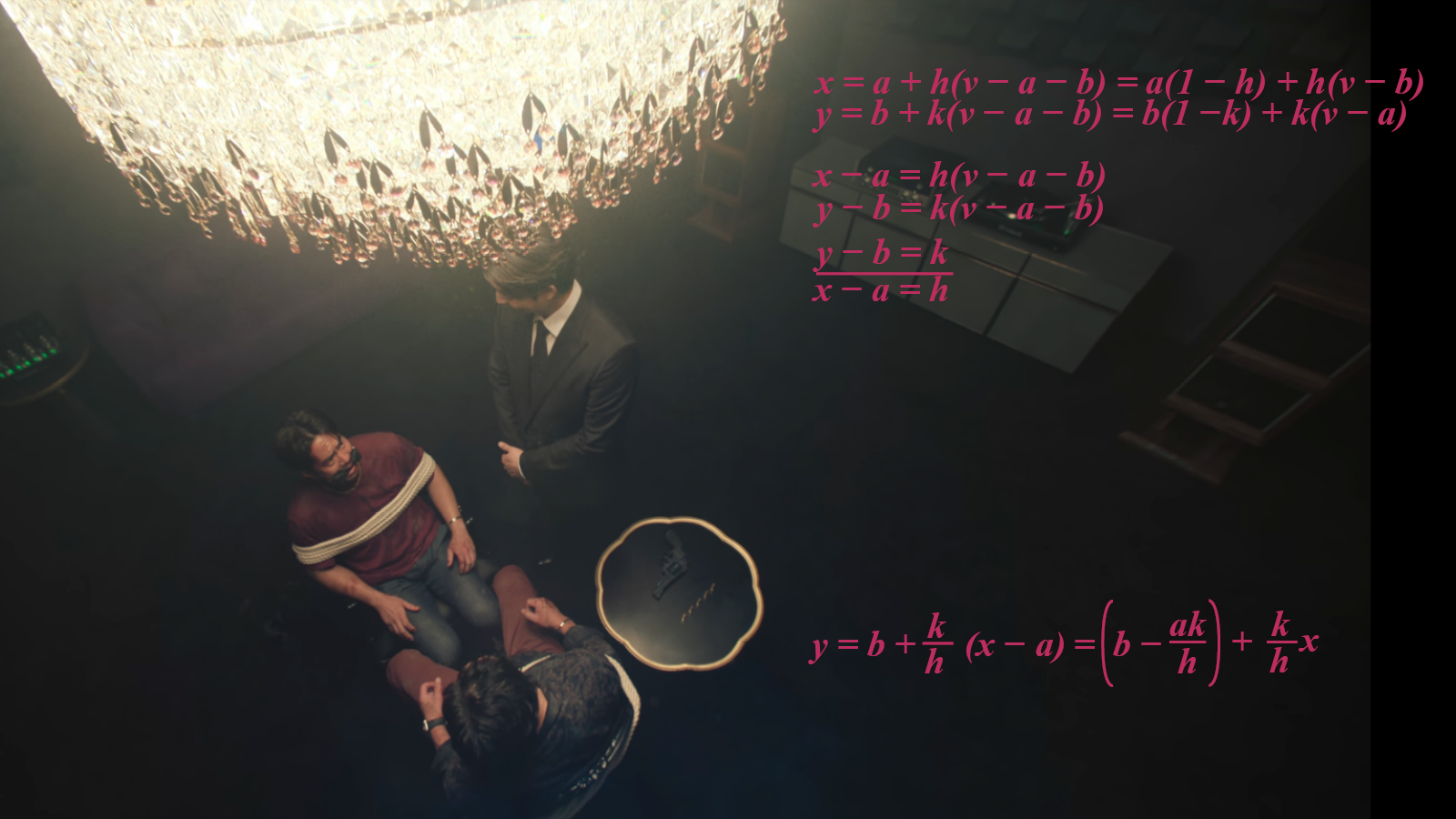Over two seasons comprised of 16 episodes, noir fiction blockbuster ‘Squid Game’ has locked in the franchise on children’s-games-with-dire-consequences movie genre.
When it comes to children’s games, there’s likely none more globally recognized than rock, paper, scissors (RPS), also known by other names such as village chief, tiger, mother of the village chief in Japan; snake, frog, slug, also in Japan; elephant, human, earwig in Indonesia; bear, man, gun in Canada; and bear, cowboy, ninja, “which may be specific to Milwaukee, USA.”
Differing symbolic protagonists aside, all RPS games share three characteristics. First, there are exactly two players. Second, both players simultaneously select and display one out of three available symbols. And third, the three symbols have a circular hierarchy of power where A defeats B, B defeats C, C defeats A, and similar symbols cancel out.
Related story: REVIEW: ‘Squid Game 2’ shocks—but also drags and leaves viewers wanting more

My interest in RPS was rekindled after watching episode one of Squid Game 2 where the game is played, but with a twist.
The modified version, called “rock-paper-scissors-minus-one,” is played in two stages. In the initial stage, each player uses both hands to simultaneously display two symbols. Then in the second and final stage, each player retracts one hand, leaving the other in play.
Given this ostensibly slight tweak, what’s the strategy players ought to follow when playing RPS-minus-one?
Probability, statistics, and the theory of games for grownups
For this inquiry, we turn to game theory.
Game theory is a collection of visual and mathematical tools used to analyze competition and cooperation among individuals and groups. My love for the discipline was first kindled after watching A Beautiful Mind (Universal Pictures, 2001), loosely based on the life story of John Nash, co-winner of the 1994 Nobel Prize in Economics.
In game theory, the betrayal of norms is called a dick move. No, just kidding; it’s called a ‘defection.’ This is what makes game theory so interesting. It shows us how to coax or compel cooperation in a cruel competitive world by teaching us a way to look into the future.
Through the years, game theory has proven to be valuable to those analyzing games of chance where players’ decisions impact outcomes. It’s been used to come up with strategies on when to, and not to, split paired hands in blackjack; when to go for a two-point conversion in American football; and how keepers can best defend the soccer goal during penalty shoot-outs; to name just a few.
Strategy for garden-variety rock, paper, scissors
Before analyzing the minus-one variant, let’s first look at the optimum strategy for garden-variety RPS. For the mathematically inclined, here’s the proof; for those who aren’t, I’ll see you at the other end of the visual.
Related story: Ready, steady, run! Here are ‘Squid Game 2’ brand collabs you won’t want to miss

In plain terms, the algebraic proof shows that in ordinary RPS, the optimum strategy is for both players to play rock one-third of the time, paper one-third of the time, and scissors one-third of the time. Most importantly, the symbols must be played in random order so that the opponent cannot exploit any patterns.
So, does this strategy guarantee a win every time?
No. RPS is fundamentally a game of chance, and conclusions from calculations like the one above hold truer and truer, the larger the number of games played. The math says that when both players adopt this one-third-random strategy, the expected outcome is that one player wins one-third of the time; the other player wins one-third of the time; and the remaining one third of games will be ties. In other words, everything ends up in a wash. However, this proportion of wins and draws can only be expected when aggregating the results of a huge number of games.
How huge? Hold my beer, while I Copilot some Python code.
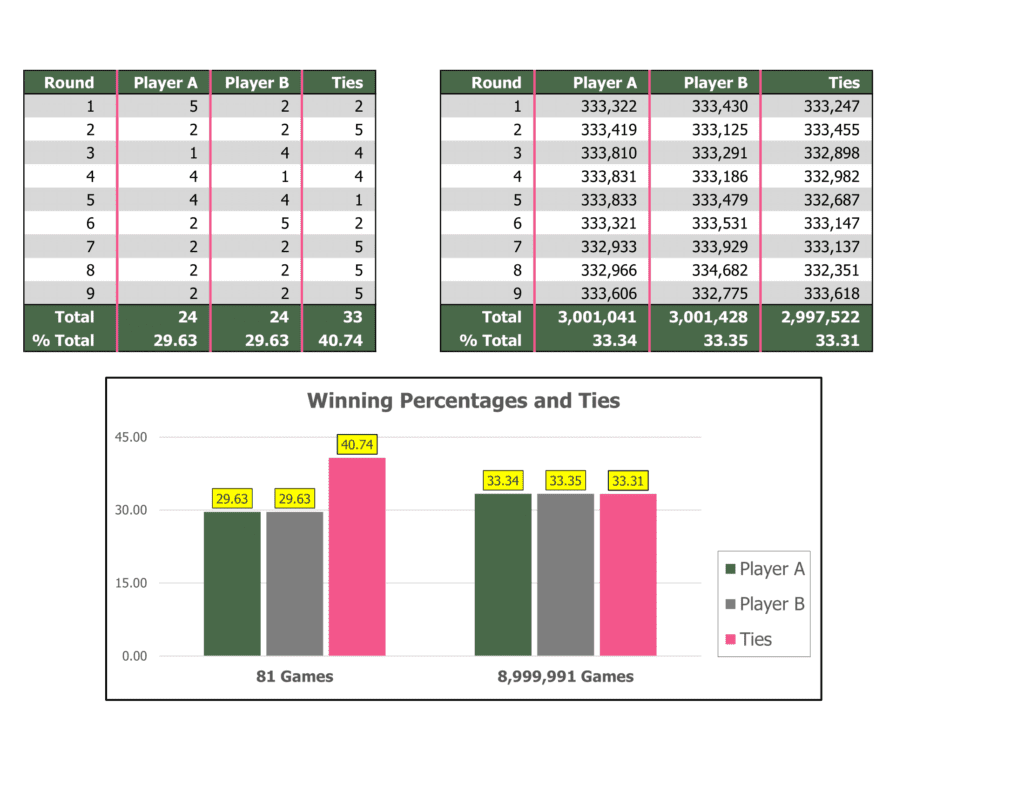
At the end of 81 games simulated by Python, both players are tied with 24 wins each, but a little over 40 percent of all games played were tied. In contrast, after 8,999,991 games Player B ekes out a 387-point win, which in the grand scheme of things is a +0.01 percent margin. Notice that at about 9 million games, the expected distribution of wins and draws begins to approach 33.33, roughly one-third when expressed as a fraction.
Rock-paper-scissors-minus-one
And now, for the main event.
First, we inventory all available move combinations, remove duplicates, and remove inferior move combinations.
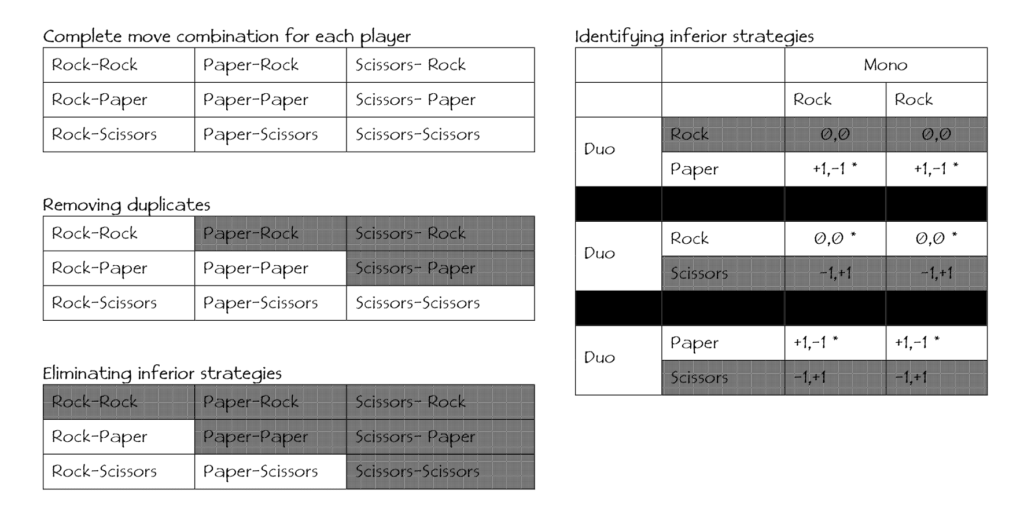
First, since each player simultaneously throws both hands, the order of the pairing doesn’t matter—that is, playing Rock-Paper, is the same as playing Paper-Rock, and so on and so forth.
Second, from among the remaining combinations, playing the same symbol with both hands is an inferior strategy. In the proof above, Mono, playing Rock-Rock, never wins, draws one-third of the time, and loses two-thirds of the time, when playing against Duo, who throws mixed pairs.
Going against Rock-Rock: Duo plays Rock-Paper, takes away Rock and wins; Duo plays Rock-Scissors, takes away Scissors and draws; Duo plays Paper-Scissors, takes away Scissors and wins.
Mono never wins, even when we know it’s possible to win, because Duo does so. In game theory parlance, throwing similar pairs is “strongly dominated,” meaning it is the worst possible choice and players are always better off opting for any of the other remaining choices—Rock-Paper, Rock-Scissors, and Paper-Scissors.
From the remaining combinations, every time both players show the same pairs, the game is a draw. In Rock-Paper mirrored, both players will retract Rock, ending up with Paper-Paper; in Paper-Scissors mirrored, both players retract Paper, ending up with Scissors-Scissors; and for Rock-Scissors mirrored, both players retract Scissors, ending up with Rock-Rock.
Notice that for each player in these cases, the symbol on one hand, defeats the symbol on the other. So, when faced with an opponent showing the same pair, the only sensible strategy is to retract the inferior hand.
With that, we’re left with a further pared down set of pair combinations.
There’s no Nash Equilibrium for the combination of Rock-Paper versus Rock-Scissors. In game theory, a Nash Equilibrium is the predicted outcome when both players try to maximize their gains, while taking into account that their opponents are trying to do the same.
So, Sam wants to play Paper, when Yup plays Rock, and Sam wants to play Rock when Yup plays Scissors, because Sam wins in both scenarios. In each case, Sam prefers a win over a draw, and a win over a loss, respectively.
Related story: Got VPN? Here are streaming recommendations to make the most of your subscription
Related story: Ten book-to-screen adaptations to add to your stream list
When losing is not an option
But what if Sam is driven by loss aversion—meaning Sam has one and only one goal, and that is to avoid losing, win and draws be damned. In fact, given the tragic consequences of defeat in Squid Game, loss aversion should be the rule rather than the exception. (For those who haven’t watched it yet, do so, then tell me I’m right. You’re welcome.)
When playing Rock, Sam has a 50 percent chance of winning and a 50 percent chance of drawing. However, when playing Paper, Sam has a 50 percent chance of winning and a 50 percent chance of losing—losing being the most tragic of outcomes. And so, with loss averse baggage in tow, Sam retracts Paper and plays Rock. On the opposing side, Yup recognizes that Sam’s only zero-loss choice is Rock, so Yup retracts Scissors, and the game ends with a Rock-Rock draw.
Applying the same principle of loss avoidance, when Sam shows Rock-Paper and Yup shows Paper-Scissors, it’s Yup now who has a 50/50 chance of winning or losing when playing Scissors, and a 50/50 chance of winning or drawing when playing Paper. In this case, Yup eliminates all chances of losing by playing Paper, and Sam, anticipating the drawing strategy, ties the game by playing Paper, too.
The last of the possible scenarios is Sam: Paper-Scissors and Yup: Rock-Scissors. For this game, Yup plays the loss-free choice, Scissors, which goes for a win or draw, Sam then draws by playing Scissors.
Caveats and conclusions
In the context of Squid Game, RPS-minus-one played perfectly as detailed above always results in a draw. However, this conclusion only holds when and only when all the following three conditions are met:
- Both players must be so deathly afraid of losing such that securing a draw is preferable to going for a win; especially when going for a win carries an equal risk of losing.
- The player with the chance to win or draw must always play for the draw, with the explicit understanding that their opponent will do the same.
- The opponent must know that the player with the chance to win or draw will always be playing for a draw.
While these three conditions are true, both players can play RPS-minus-one in perpetuity, drawing for all eternity. Break any of these conditions and everything goes to hell in a handbasket.
Related story: 5 must-read novels by South Korean writers
Related story: All eyes on Asia

For example, in Sam: Paper-Scissors; and Yup: Rock-Scissors. It’s Yup who has a chance to forgo the chance to win and secure a draw with Scissors. But in a cruel twist, Yup suddenly decides to go Rock. Now Sam, expecting a Scissors-Scissors draw, throws Scissors which loses to Rock.
In game theory, this betrayal of norms is called a dick move. No, just kidding; it’s called a “defection.” Since RPS-minus-one is played over multiple rounds, trust is the only glue that holds together cooperative play. A defection from either player threatens to eradicate any chance of further cooperation. Extrapolated into real world terms, if you believe that someone who screwed you over once before won’t do it again, there’s a bridge I want to sell you at a bargain basement price.
This is what makes game theory so interesting. It shows us how to coax or compel cooperation in a cruel competitive world by teaching us a way to look into the future.
And, win, lose, or draw, learning to look into the future will always be an indispensable part of the game called life.